다익스트라(Dijkstra) 알고리즘

다익스트라 알고리즘은 최단거리를 구할 때 사용한다 bfs도 최단거리를 구할때 사용하지만 차이점은 bfs는 단위길이 모든 간선의 가중치가 서로 같을 때 이용가능하다 다익스트라 알고리즘은 노드 사이 간선의 가중치가 다를 때 사용한다

만약 간선의 가중치가 다를 때 모두 동일하게 간선을 쪼개서(추가적인 노드가 생성 2인 간선에 노드를 1개 추가해서 1,1로 만듦) bfs를 이용할 수도 있다

---

다익스트라

다익스트라 알고리즘은 시작 정점에서 모든 노드의 최단거리를 구하는것이다 원리는 하나의 노드에서 이동가능한 노드를 찾은 뒤 이동 가능한 노드중에서 거리의 값이 가장 작은 노드로 이동(방문 처리를 한다)해서 다시 그 노드에서 이동 가능한 노드(방문 하지 않은 노드중)를 찾고 거리의 값이 가장 작은 노드로 이동 이것을 반복한다 모든 노드를 방문 한다면 각 노드에는 시작 정점에서 도달할 수 있는 최단거리가 입력 되게 된다

1. 시작 노드 설정

2. 해당 노드에서 이동할 수 있는 노드 찾기

3. 이동 가능한 노드 중 거리가 가장 짧은 노드로 이동, 이동한 거리를 이동 노드에 넣음

4. 노드 방문 처리

   2->3->4를 반복 처리해서 모든 노드를 방문하면 끝이난다

 

리스트로 구현

 

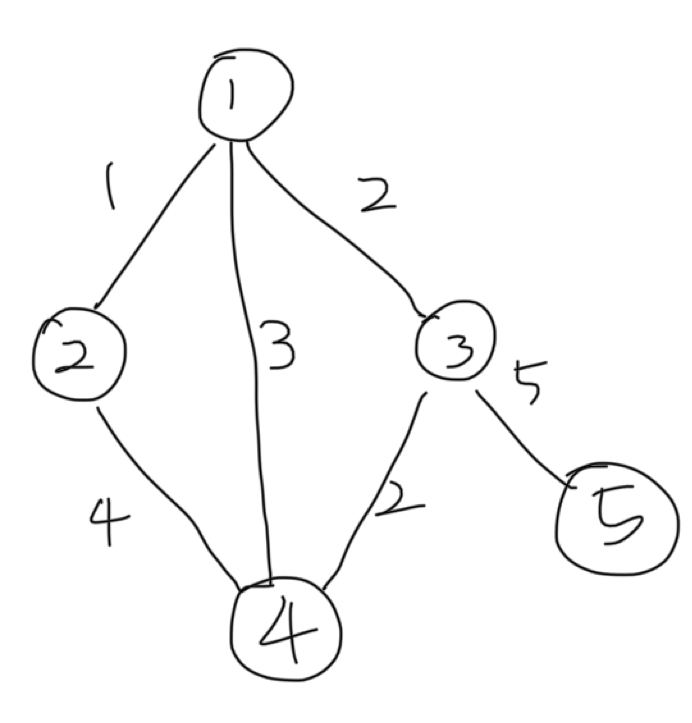
사진과 같은 노드가 존재할 때 시작 점을 1로하자 만약 시작점에서 도달 할 수 없으면 INF로 표기

 

처음 노드에서 이동 가능한 경우를 리스트에 넣음

인덱스 0	1	2	3	4	5
거리	0	1	2	3	INF
방문여부	1	0	0	0	0

다음 노드는 이동 거리 값이 가장 작은 노드를 선택한다 여기서는 2를 선택

인덱스 0	1	2	3	4	5
거리	0	1	2	min(5,3)	INF
방문여부	1	1	0	0	0

2에서 이동가능한 노드는 4 이다 노드 4에 값이 이미있으므로 앞으로 들어올 값과 비교해서 더 작은 값을 넣어야 한다

1+4와 3을 비교하면 원래 값이 더 작으므로 3이 유지된다 2에서 이동 가능한 노드는 4이므로 다음 노드는 4

인덱스 0	1	2	3	4	5
거리	0	1	min(5,2)	3	INF
방문여부	1	1	0	1	0

노드 4에서 이동 가능한 경우는 3만 존재 (다른 노드는 이미 방문처리가 됐음) 노드 3은 3+2와 2를 비교해 작은 값을 갖는다 4에서 이동 가능한 경우는 3 뿐이므로 노드 3으로 이동

인덱스 0	1	2	3	4	5
거리	0	1	2	3	7
방문여부	1	1	1	1	1

노드 3에서 이동 가능한 경우는 노드 5 밖에 없다 노드 5에는 값이 없으므로 2+5가 들어간다 다음은 5번 노드로 이동하는데 5번 노드에서 더 이상 방문 가능한 곳이 없어 다익스트라 알고리즘은 끝난다

 

 

---

파이썬 구현

2중 리스트로 구현

import sys  #우선순위 큐를 사용하지 않는 다익스트라
input = sys.stdin.readline
INF = int(1e9)#무한을 표시

n, m = map(int, input().split()) #n개의 노드와 ,m개의 간선정보
start = int(input()) #시작점
# 주어지는 그래프 정보 담는 N개 길이의 리스트
graph = [[] for _ in range(n+1)]
#노드 인댁스 0은 사용하지 않는다
visited = [False] * (n+1)  # 방문처리 기록용
distance = [INF] * (n+1)   # 거리 테이블용

for _ in range(m):
    a, b, c = map(int, input().split())
    graph[a].append((b, c))

# 방문하지 않은 노드이면서 시작노드와 최단거리인 노드 반환
def get_smallest_node():
    min_value = INF
    index = 0
    for i in range(1, n+1):
        if not visited[i] and distance[i] < min_value: #방문하지 않고 INF보다 작을떄
            min_value = distance[i]
            index = i
    return index

# 다익스트라 알고리즘
def dijkstra(start):
    # 시작노드 -> 시작노드 거리 계산 및 방문처리
    distance[start] = 0 #시작노드는 0
    visited[start] = True
    # 시작노드의 인접한 노드들에 대해 최단거리 계산
    for i in graph[start]: #i에는 도착지, 간선값이 들어간다
        distance[i[0]] = i[1] #도착지에 간선값이 들어감

    # 시작노드 제외한 n-1개의 다른 노드들 처리
    for _ in range(n-1):
        now = get_smallest_node()  # 방문X 면서 시작노드와 최단거리인 노드 반환
        visited[now] = True        # 해당 노드 방문처리
        # 해당 노드의 인접한 노드들 간의 거리 계산
        for next in graph[now]:
            cost = distance[now] + next[1]  # 지금 노드까지 최단거리 + 다음 노드 거리
            if cost < distance[next[0]]:    # cost와 다음 노드에 시작->이동노드 거리가 있다면 비교
                distance[next[0]] = cost    #값이 없다면 INF가 들어가있어 실행 cost가 더 작으면 값은 바꾼다

dijkstra(start)

for i in range(1, n+1):
    if distance[i] == INF:
        print('INF')
    else:
        print(distance[i])

이 알고리즘에서는 최단거리의 노드를 구할때 get_smallest_node 함수에서 선형탐색을 이용해 다음 노드를 찾으므로 n,m이 커질 수록 시간이 오래 걸린다 따라서 이 함수 대신 우선순위 큐를 이용해서 풀이를 할 수 있다

 

 

우선순위큐(힙) 구현

import sys #우선순위 큐를 이용해서 시간복잡도를 단축
import heapq #파이썬에서 힙은 최소힙으로 구현되어 있다
input = sys.stdin.readline
n, m = map(int, input().split())
start = int(input())
INF = int(1e9) #무한 표시

distance = [INF] * (n+1)
graph = [[] for _ in range(n+1)]

for _ in range(m):
    a, b, c = map(int, input().split())
    graph[a].append((b, c))
# 위와 같음 visted 리스트만 없어짐

def dijkstra(start):
    q = []
    heapq.heappush(q, (0, start))  # 시작노드 정보 우선순위 큐에 삽입
    distance[start] = 0            # 시작노드 거리 0
    while q:
        dist, node = heapq.heappop(q)
        if distance[node] < dist: #큐에서 뽑은 값의 최단거리와 거리를 비교
            continue
        
        for next in graph[node]:#인접 노드를 탐색
            cost = distance[node] + next[1]   # 지금 노드까지 최단거리 + 다음 노드 거리cost와 다음 노드에 시작->이동노드 거리가 있다면 비교
            if cost < distance[next[0]]:      # 값이 없다면 INF가 들어가있어 실행 cost가 더 작으면 값은 바꾼다
                distance[next[0]] = cost
                heapq.heappush(q, (cost, next[0])) #여기서 cost는 거리가 되지만 우선순위도 의미
 

dijkstra(start)

for i in range(1, len(distance)):
    if distance[i] == INF:
        print('INF')
    else:
        print(distance[i])

이 방법은 파이썬의 heapq모듈에 대해 알고 있어야한다

heapq는 파이썬에서 힙을 이용할 때 사용하는 모듈이고 기본적으로 최소 힙이 구현되어 있다 따라서 heapq.heappush( 힙 ,( 우선순위 , 들어갈 값 ) ) 이렇게 만들어져 있어서 우선순위는 0>1>2>3 … 이렇게 적용된다 따라서 우선 순위부분에 노드사이 최단거리를 입력하면 짧을 수록 먼저 힙에서 나오게 된다 최단거리 노드를 찾는 과정이 줄어들어 시간이 단축된다