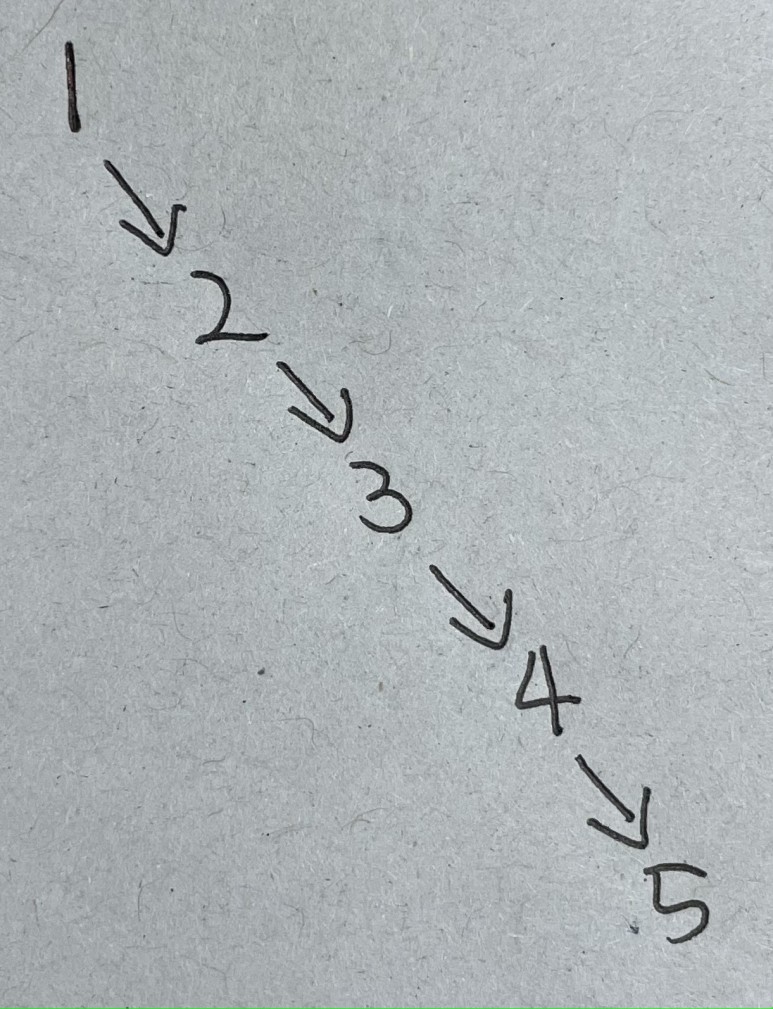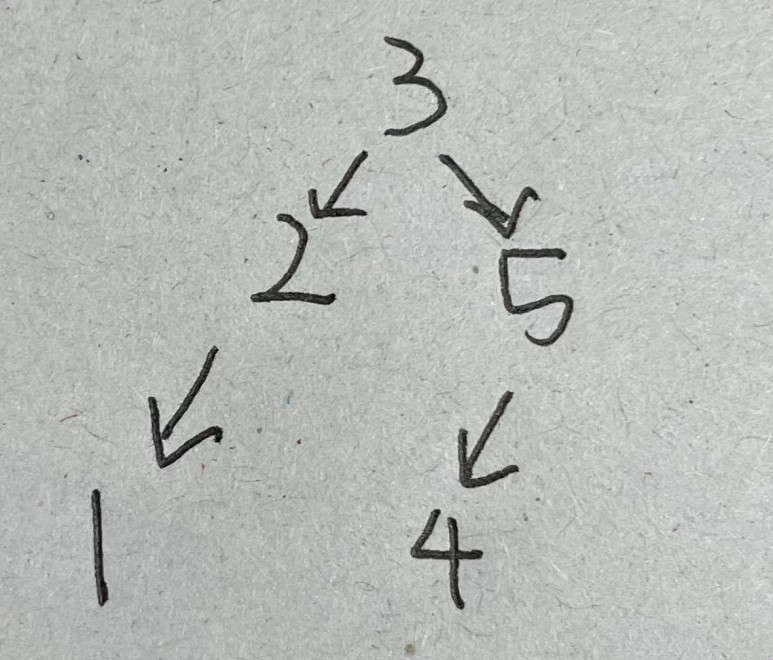데이터 구조(4)-이중연결리스트 이진트리
이중 연결 리스트
- 연결 리스트는 연결 리스트를 변형한것으로 각 노드에 2개의 링크(주소 기록)가 있다
- 한 링크는 다음 노드를 가리키고 다른 한 링크는 앞 노드를 가리킨다
- 처음과 마지막 노드를 모두 기록한다
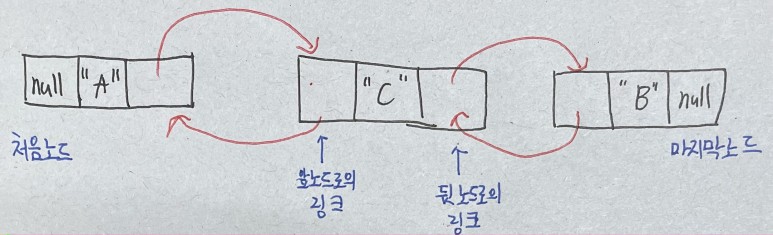
이중 연결 리스트는 처음 노드와 마지막 노드를 모두 가지고 있으므로 리스트 앞과 끝에 모두 O(1)에 접근 가능하다
따라서 양 끝에서 O(1)로 데이터 추가/삭제가 가능하다
트리
순서 유지와 빠른 검색과 삽입, 삭제가 가능한 자료 구조 이진 트리
트리도 노드기반 자료 구조이지만 트리의 각 노드는 여러 노드로의 링크를 포함 할 수 있다
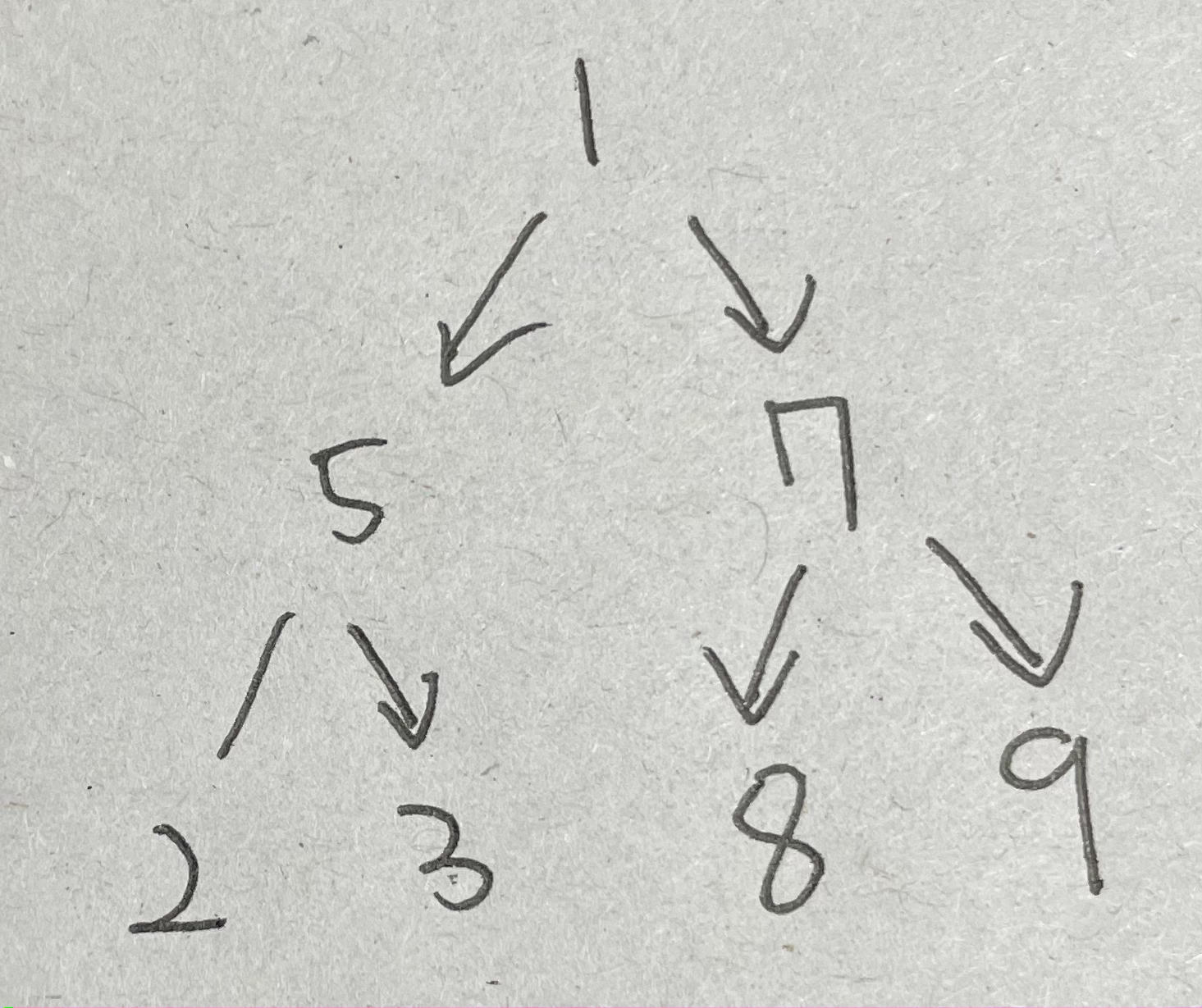
- 가장 상위 노드 위에서는 1을 루트라고 부름
- 1을 5,7의 부모 5,7은 1의 자식이 된다
- 트리에는 레벨이 있는데 위는 세 레벨이다
이진 트리
위에 조건을 모두 가지고 추가적인 조건이 있다
- 각 노드의 자식은 0개,1,2개이다
- 한 노드에 자식이 둘이면 한 자식은 부모보다 작은 값을, 다른 자식은 부모보다 큰 값을 가져야 한다
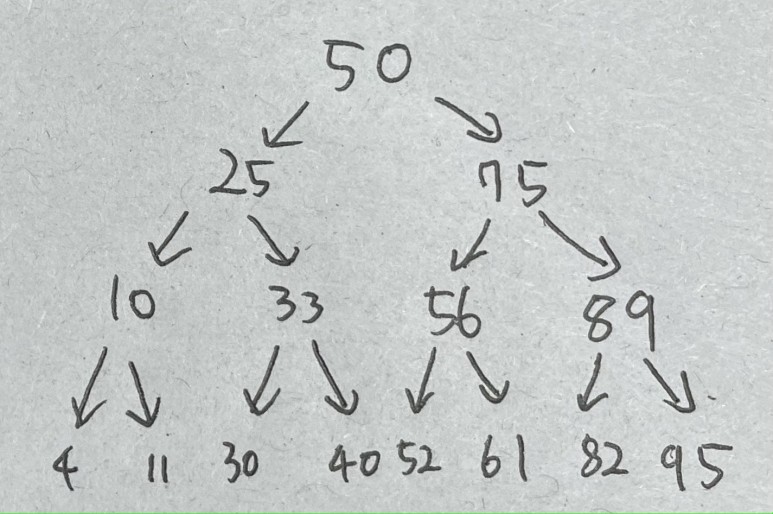
이진 트리 검색
검색 알고리즘
1 노드의 값 확인
2 찾는 값이면 끝 아니면 다음으로 넘어감
3 찾고 있는 값이 현재 노드보다 작으면 왼쪽 하위 트리 검색
4 찾고 있는 값이 현재 노드보다 크면 오른쪽 하위 트리 검색
이진 트리 검색에서는 O(log N)의 시간이 걸린다
각 단계를 수행 할때마다 남은 공간중 반을 제거하기 때문이다 이진 검색과 비슷하다
이진 트리 삽입
먼저 데이터가 들어갈 자리를 찾기위해 검색을 진행한다
그 뒤에 삽입을 하면 된다
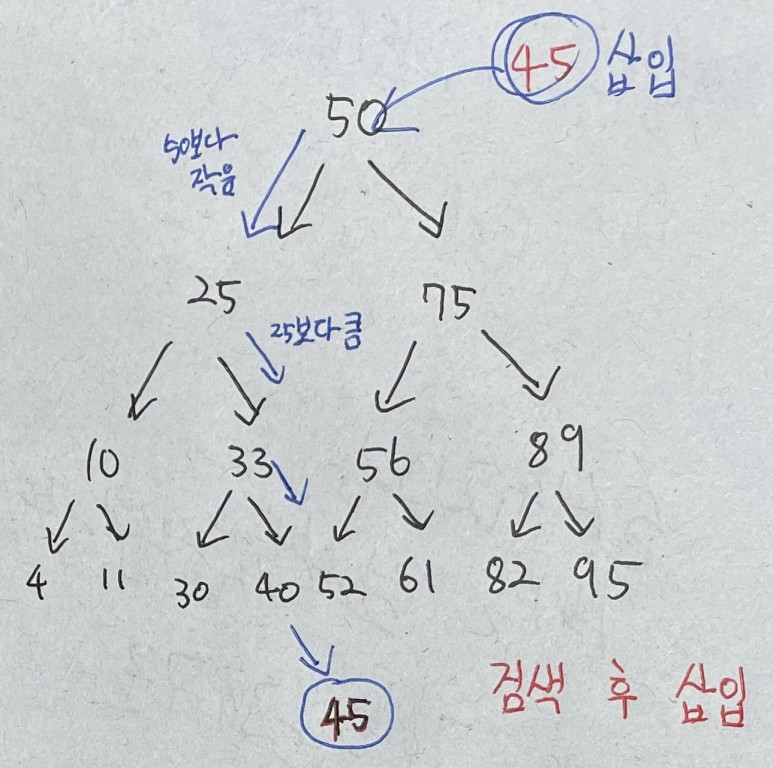
삽입은 검색 + 1단계이다 따라서 O(log N)이 된다
트리는 무작위로 정렬된 데이터로 트리를 생성해야 균형잡힌 트리가 된다
이진 트리 삭제
삭제 또한 검색 후 삭제이다 하지만 자식노드의 개수에 따라 방법이 바뀐다
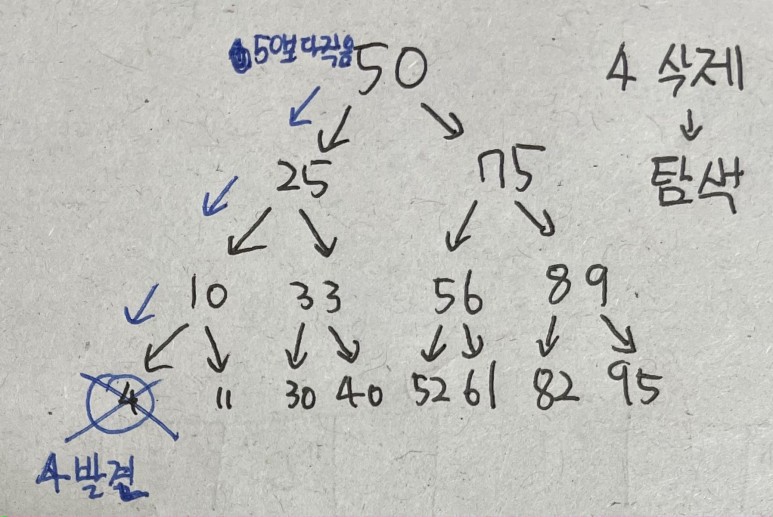
자식 노드가 0개이면 그냥 삭제한다
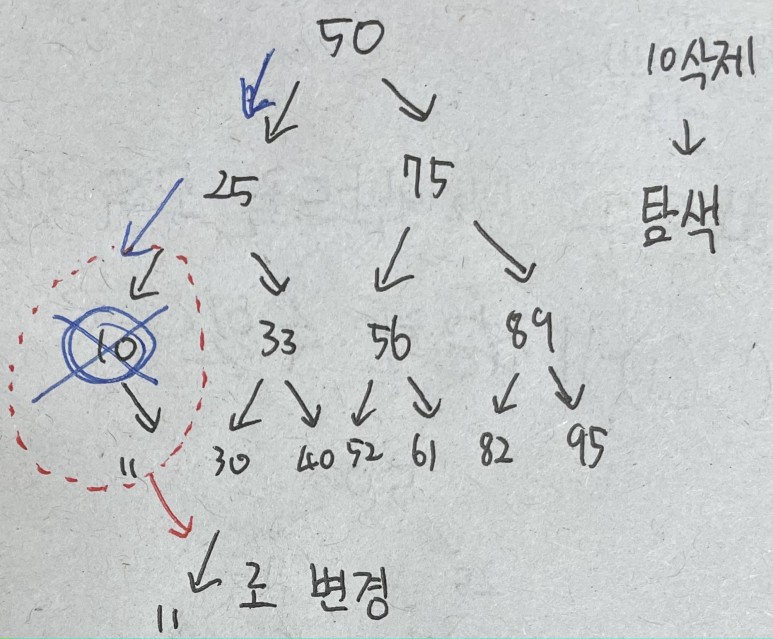
자식 노드가 1개인 경우 부모 노드의를 지우고 그 위치에 남은 자식 노드가 들어간다
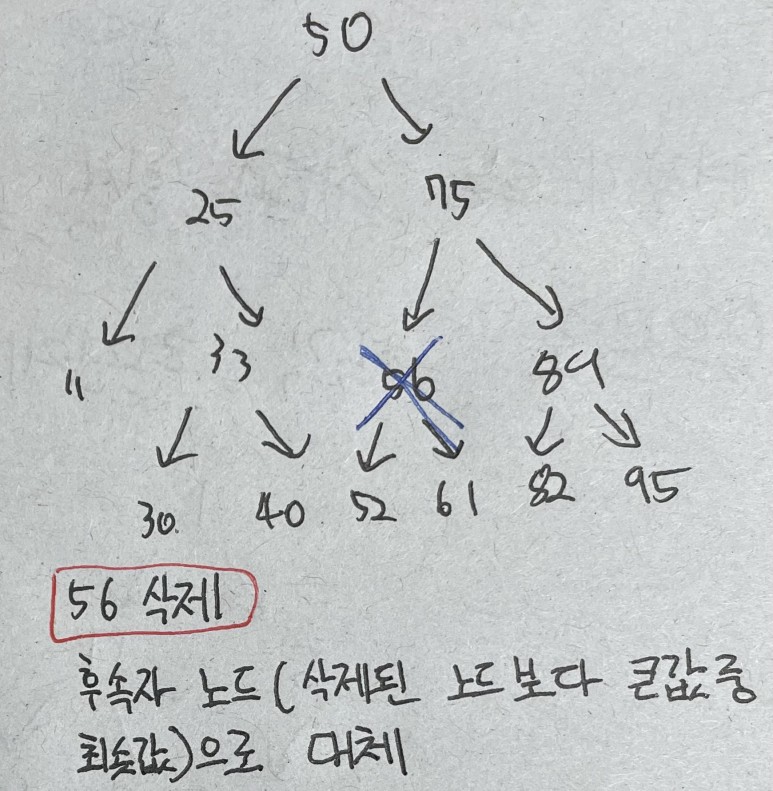
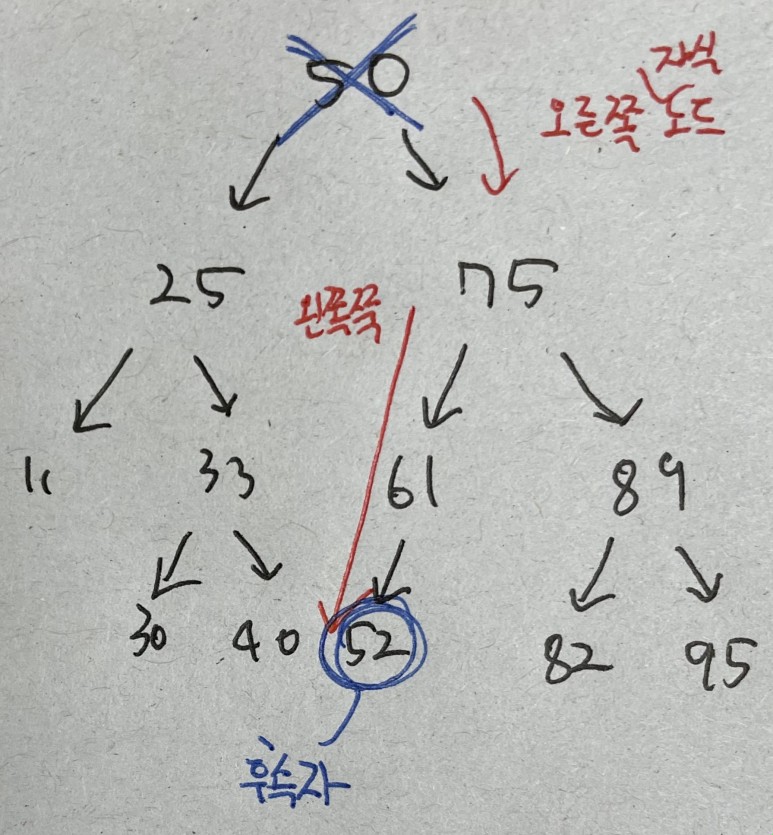
자식 노드가 2개이면 후속자 노드(삭제된 노드보다 큰 값중 최솟값)로 교체된다
위에서는 56자리에 61이 들어가는 것으로 끝난다
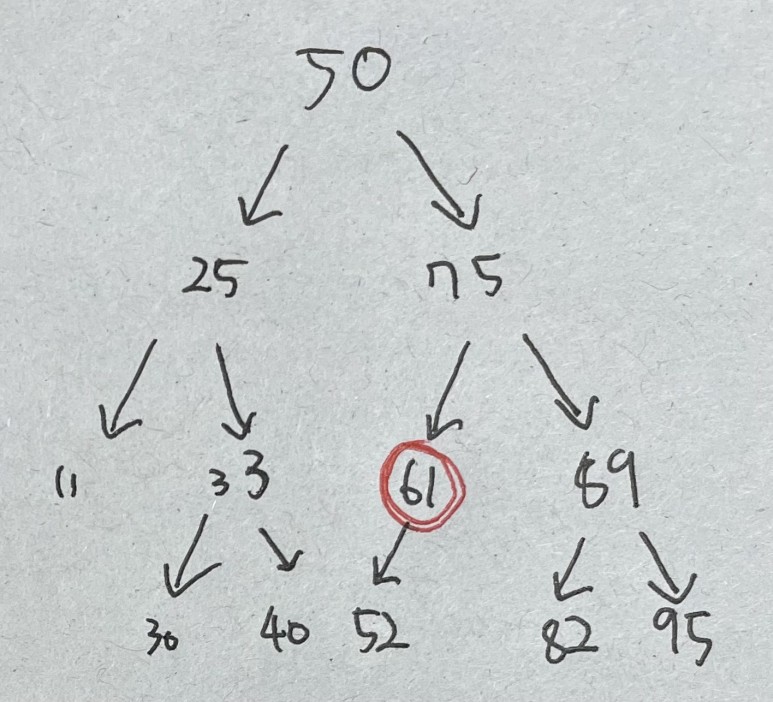
컴퓨터는 후속자 값을 찾을때 삭제된 노드 오른쪽 자식중에서 그 자식중 왼쪽 자식을 따라 계속해서 내려간다 더 이상 자식이 없을 때까지
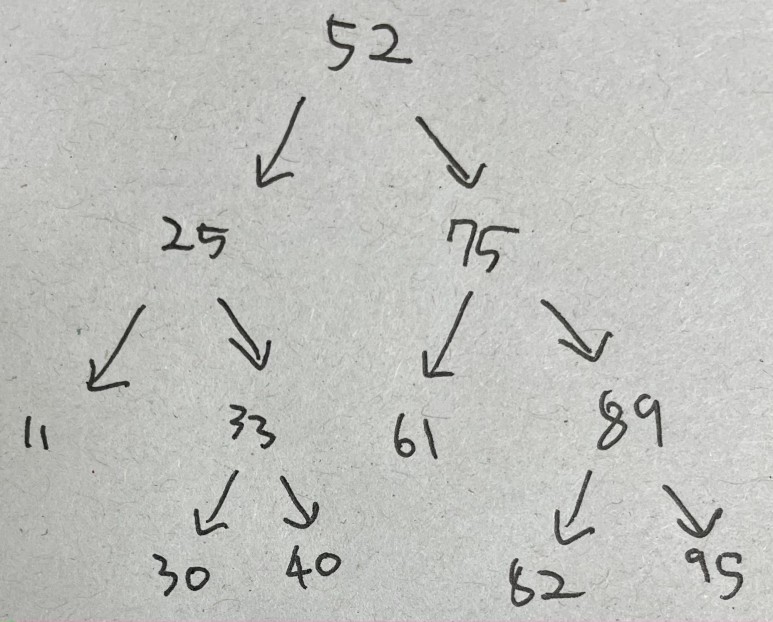
루트 노드를 삭제하면 후속자 노드를 찾아야한다 위에서 52라는 후속자 노드를 찾아 루트 노드에 넣으면 오른쪽 사진 처럼 이진 트리가 배치된다
삭제 알고리즘
- 삭제할 노드에 자식이 없으면 그냥 삭제한다
- 삭제할 노드에 자식이 1개면 노드를 삭제하고 자식은 삭제된 노드 자리에 넣는다
- 자식이 둘인 노드를 삭제할 때는 삭제된 노드를 후속자 노드롤 대체한다
ㄴ 후속자 노드에 오른쪽 자식이 있으면 후속자 노드의 원래 자리에 넣는다