백준 1504번 특정한 최단경로

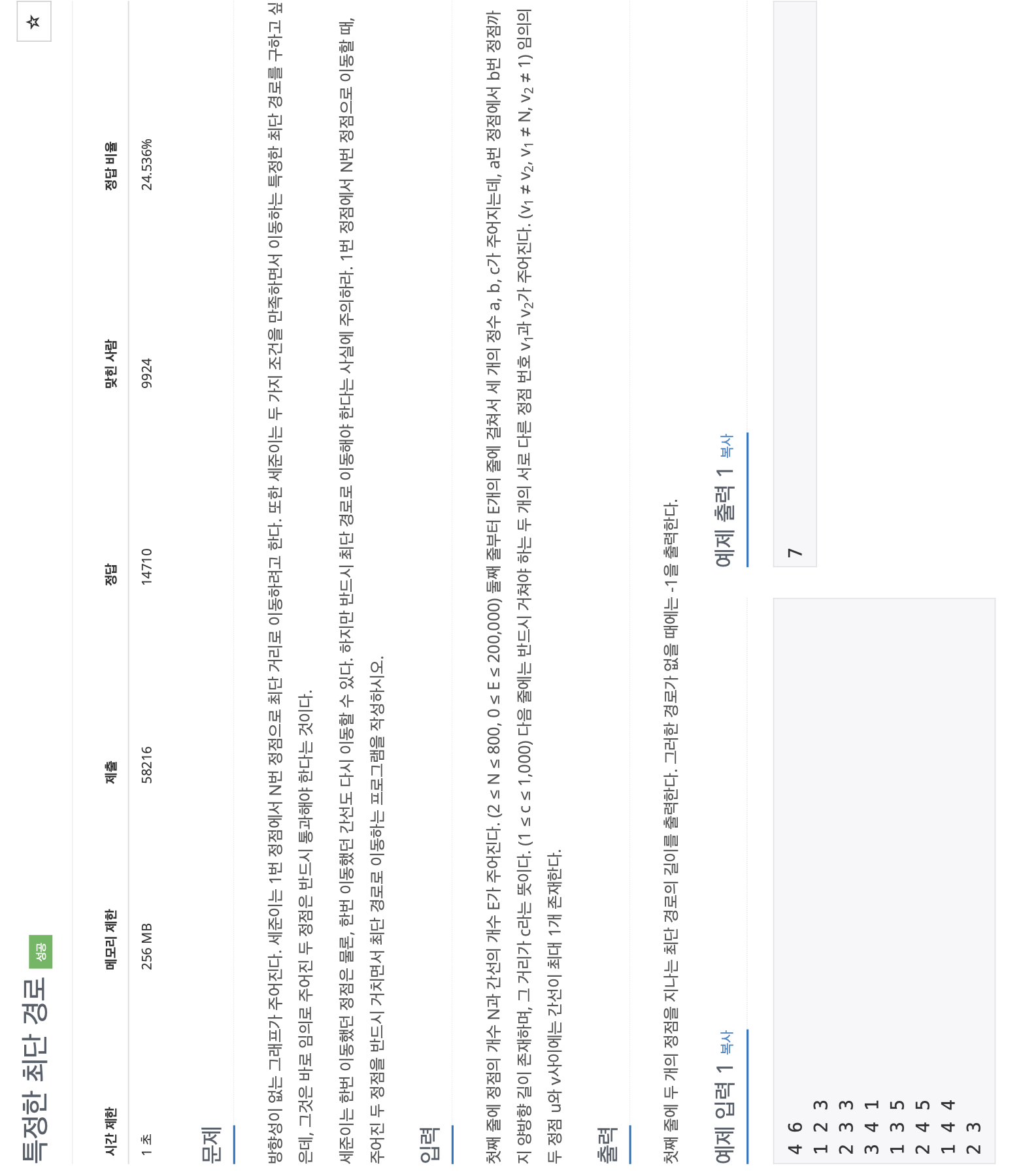
기본적인 다익스트라 문제에서 특정 조건 2개가 추가된 문제이다

다익스트라 알고리즘에서 양방향으로 이동 할 수 있도록 입력을 받을때 반대 방향 그래프로 같이 넣어준다

이 문제서는 두 점을 추가로 주어서 그 점을 경유하는 최단거리를 구하는 것이다 이 두번째 조건을 해결하기 위해 경유 정점 2개를 기준으로 경유를 통해 나올 수 있는 최단거리를 예상하면 2가지 경우만 나온다

(1) start -> v1 -> v2 -> goal 또는 (2) start -> v2 -> v1 -> goal 이렇게 2가지 경우만 존재한다 두가지 경우으 값을 비교해서 최단거리를 출력한다

각각의 사이 거리의 최단거리를 합하면 되는데 다익스트라 알고리즘은 한점에서 모든 점까지 최단거리를 구하는것이다

따라서 다익스트라 알고리즘을 v1출발지, v2출발지로 2개를 구하면 문제를 해결 할 수 있다

 

 

 

import sys #우선순위 큐를 이용해서 시간복잡도를 단축
import heapq
input = sys.stdin.readline
n, m = map(int, input().split())
start = 1
INF = int(1e9)

graph = [[] for _ in range(n+1)]

for _ in range(m):
    a, b, c = map(int, input().split())
    graph[a].append((b, c))
    graph[b].append((a, c))

v1,v2 = map(int,input().split()) #중간에 경유해야된는곳

def dijkstra(s):
    distance = [INF] * (n+1)

    q = []
    heapq.heappush(q, (0, s))  # 시작노드 정보 우선순위 큐에 삽입
    distance[s] = 0           # 시작노드->시작노드 거리 기록

    if s == v1:
        distance[0] = v2
    else:
        distance[0] = v1

    while q:
        dist, node = heapq.heappop(q)
        # 큐에서 뽑아낸 거리가 이미 갱신된 거리보다 클 경우(=방문한 셈) 무시
        if distance[node] < dist:
            continue
        # 큐에서 뽑아낸 노드와 연결된 인접노드들 탐색
        for next in graph[node]:
            cost = distance[node] + next[1]   # 시작->node거리 + node->node의인접노드 거리
            if cost < distance[next[0]]:      # cost < 시작->node의인접노드 거리
                distance[next[0]] = cost
                heapq.heappush(q, (cost, next[0]))


    return distance[start],distance[distance[0]],distance[n]


dist1 = list(dijkstra(v1))
dist2 = list(dijkstra(v2))

best_dist1 = dist1[0] + dist1[1] + dist2[2]
best_dist2 = dist2[0] + dist2[1] + dist1[2]

if best_dist1 < INF or best_dist2 < INF:
    if best_dist1 < best_dist2:
        print(best_dist1)
    else:
        print(best_dist2)
else:
    print(-1)