백준 1707번 이분 그래프

이분 그래프란 인접한 정점끼리 서로 다른색을 칠해서 모든 정점을 두가지로 칠할 수 있을때 이분 그래프라고 한다

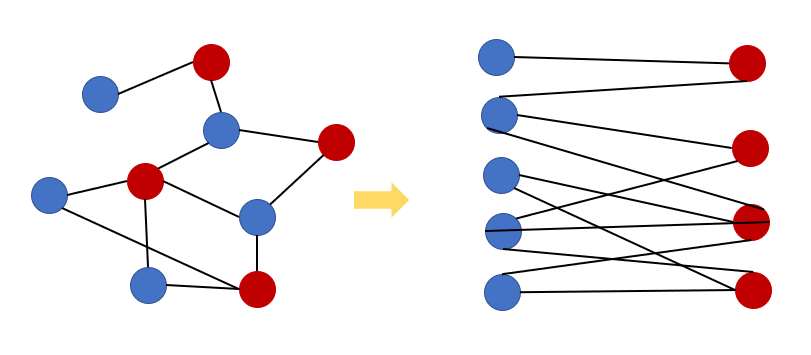
위 그림과 같이 파란색끼리는 연결이 안되고 빨간색끼리도 연결이 안되지만 서로 연결되어 있는 그래프를 이분 그래프라고 한다

정점과 간선의 정보를 받아서 이분 그래프인지 판단해야한다

이분 그래프 판단 방법으로 대표적 2개가 있다 dfs와 bfs를 통해서 해결할 수 있는데 bfs를 이용해서 같은 위치(같은 최단거리)일때 서로 연결 되어있으면 안된다라고 생각 하고 풀었다 하지만 같은 위치의 정점을 또 모두 if문을 돌리기에는 시간 초과가 날것 같았다

그래서 정점하나가 갈수 있는곳을 찾고 방문하지 않은 곳이라면 지금과 반대의 -1or1을 넣는다 만약 방문했다면 지금의 상태와 반대가 되는지 확인 반대가 아니라면 이분그래프가 아니므로 바로 판단 가능하다

import sys
from collections import deque
input = sys.stdin.readline

def bfs(a):#bfs 함수
    q= deque()
    q.append(a)
    ans[a] = 1
    while q:
        x = q.popleft()
        for i in line[x]:
            if ans[i] == 0:
                ans[i] = -ans[x]
                q.append(i)
            elif ans[i]==ans[x]:#지금과 같은 정보를 가짐 바로 break
                    return False
    return True
                
test = int(input())

for _ in range(test):
    q = deque()
    
    V,E= map(int,input().split()) #정점V와 간선E 
    line =[[] for _ in range(V+1)]
    ans = [0]*(V+1)
    flag = 1
    
    for i in range(E):
        u,v = map(int,input().split()) #간선 정보
        line[u].append(v)
        line[v].append(u)

    for i in range(1,V+1):
        if ans[i] == 0:
            if not bfs(i):
                flag=-1
                break
            
    print('YES' if flag == 1 else "NO")