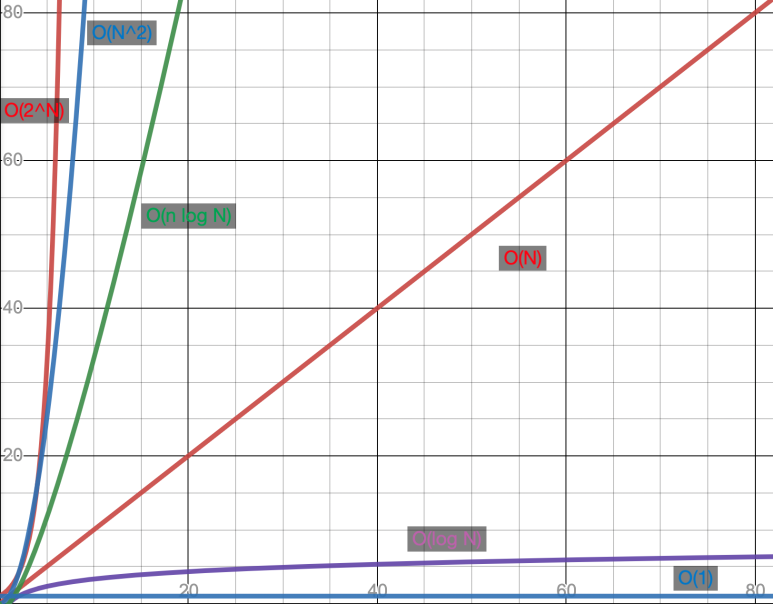
빅 오( Big O ) 표기법
컴퓨터 과학자들은 알고리즘의 효율성을 간결하고 일관된 언어로 설명하기 위해 수학적 개념을 차용했다
이 개념을 형식화한 표현을 빅 오 표기법이라고 부른다
데이터가 증가할수록 단계 수가 어떻게 변하는지를 표현함
빅 오 표현법은 최악을 표기한다 (단계 수가 빅 오보다 작을 수 있다)
- 최대 지수만 표현 (영향이 제일 큰것만 표시)
- 상수항은 무시한다
O(1)
O(1)은 데이터 크기와 상관없이 알고리즘에 필요한 단계 수가 일정하다는 뜻이다
ex) 배열 읽기, 배열의 끝 삭제와 삽입, 연결 리스트 처음 삭제와 삽입
O(N)
O(N)은 배열 내에 N 개의 원소가 있을 때 알고리즘을 끝내는데 N 개의 단계가 필요함을 뜻한다
ex) 배열 처음에 삽입 삭제
상수 시간과 선형 시간
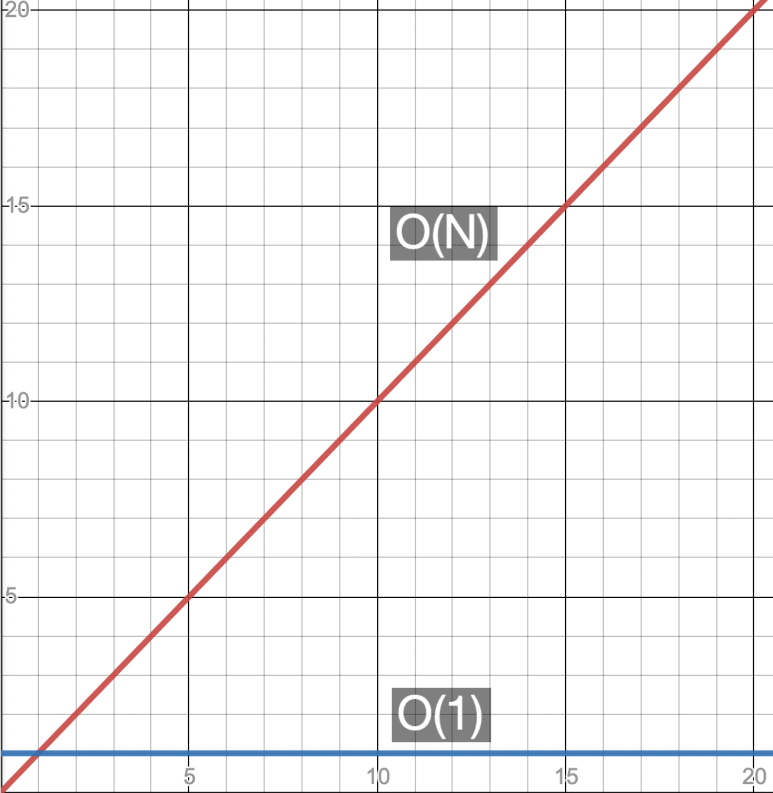
O(N)은 x 증가량과 y 증가량이 같은 대각선이 그려진다 데이터가 많아질수록 단계 수도같이 증가한다
이러한 이유로 O(N)을 선형 시간이라고도 부른다
O(1)은 완벽한 수평선이다 데이터의 개수에 상관없이 알고리즘에 걸리는 단계가 일정하다 이러한 이유로
O(1)을 상수 시간이라고 부른다
O(log N)
O(log N)은 O(1)과 O(N) 사이의 어딘가이다 오 로그 N으로 읽는다
정렬된 배열에서는 선형 탐색보다 이진 탐색이 훨씬 빠른 것을 알고 있다 선형 탐색 O(N)보다 빠르지만 그렇다고 O(1)은 될 수 없다 왜냐하면 데이터가 증가할수록 단계 수도 증가하기 때문이다
이진 검색은 O(N)과 O(1) 사이인데 이진 검색은 빅 오 표현으로
로그 시간의 시간 복잡도라고 말한다
데이터가 두 배로 증가할 때 한 단계가 늘어나는 알고리즘을 표현한다
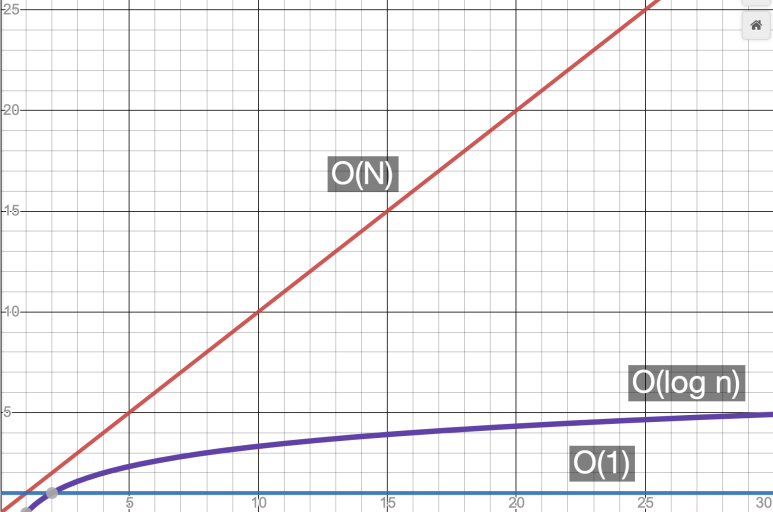
O(log n) 해석
log n에서 log는 밑이 2인 로그인데 편의를 위해 생략한 것이다 O(log N)은 데이터 원소가 N 개 있으면 log{2}N 단계가 걸린다는 것이다 N이 8이면 3단계가 된다 특정 항목을 찾을 때까지 원소를 반으로 나누어 범위를 좁혀나간다 O(N)에 비해서 O(log N)은 데이터가 두 배 늘어났을 때 딱 한 단계만 더 필요하다
위에서 나온 표현 말고도 여러가지를 빅 오 표현법으로 표현한다